Available in a git repository.
Repository: sawsim
Browsable repository: sawsim
Author: W. Trevor King

Over the past week I've been working up a Python framework for my sawsim simulator, to allow parallel execution on a variety of systems. I think I've got the kinks worked out now, and sawsim (or anything else that can subclass pysawsim.manager.Job can now be transparently executed in parallel using any of

Python's threading module (the thread manager).
Python's multiprocessing module (the subproc manager).
MPI (via mpi4py, the mpi manager).
PBS (via pbs_python, the pbs manager).

Most of the difficulty is in handling systems where not all of these approaches are viable, (e.g. Python 2.5, so no multiprocessing module, or an SMP host that wants to use subproc without installing mpi4py or pbs_python). I also ran up against Python's issue5155 when I tried to test the subproc manager from within a:

$ nosetests --with-doctest --doctest-tests --processes $N pysawsim

on a Python 2.6.2 system (it was fixed by 2.6.3).

Note that Python's GIL restricts threads to a single core. This means that the thread manager is basically decorative, but I wrote it anyway because it forms the basis of several other managers, and it's the only manager that will definitely work on Python 2.5.

Available in a git repository.
Repository: sawsim
Browsable repository: sawsim
Author: W. Trevor King

Introduction

My thesis project investigates protein unfolding via the experimental technique of force spectroscopy. In force spectroscopy, we mechanically stretch chains of proteins, usually by pulling one end of the chain away from a surface with an AFM.

For velocity clamp experiments (the simplest to carry out experimentally), the experiments produce "sawtooth" force-displacement curves. As the protein stretches, the tension increases. At some point, a protein domain unfolds, increasing the total length of the chain and relaxing the tension. As we continue to stretch the protein, we see a series of unfolding peaks. The GPLed program Hooke analyzes the sawtooth curves and extracts lists of unfolding forces.

Lists of unfolding forces are not particularly interesting by themselves. The most common approach for extracting some physical insights from the unfolding curves is to take a guess at an explanatory model and check the predicted behavior of the model against the measured behavior of the protein. If the model does a good job of explaining the protein behavior, it might be what's actually going on behind the scenes. Sawsim is my (published!) tool for simulating force spectroscopy experiments and matching the simulations to experimental results.

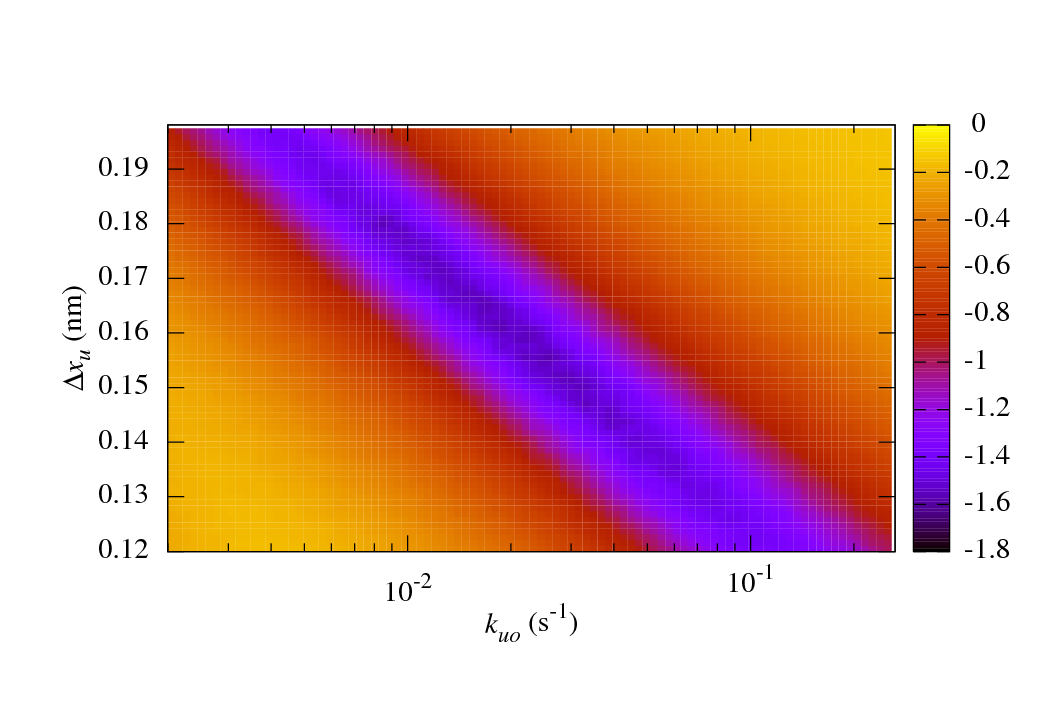
The main benefits of sawsim are its ability to simulate systems with arbitrary numbers of states (see the manual) and to easily compare the simulated data with experimental values. The following figure shows a long valley of reasonable fits to some ubiquitin unfolding data. See the IJBM paper (linked above) for more details.

Getting started

Sawsim should run anywhere you have a C compiler and Python 2.5+. I've tested it on Gentoo and Debian, and I've got an ebuild in my Gentoo overlay. It should also run fine on Windows, etc., but I don't have access to any Windows boxes with a C compiler, so I haven't tested that (email me if you have access to such a machine and want to try installing Sawsim).

See the README, manual, and PyPI page for more details.

I recently learned about distributed versioning systems like Git, Mercurial, Bazaar, etc., and I moved my sawsim development to Git from Subversion (instructions at Simplistic Complexity).

The benefit of a distributed version control system for me is that it removes the need for a central repository. That means that if Bob pulls my code and makes some changes, and Alice pulls my code and makes some other changes, Bob and Alice can get together and merge their code without my knowledge/permission/whatever. I think this will lead to more lively and effective code.

As for picking Git, I'm sure all would be sufficient for my needs, and Git seemed more like my style.

Alright, my tensions now agree with Prof. Yang's simulated tensions for 4-domain ubiquitin poly-proteins. Presumably our Bell-model-predicted histograms will match up as well, but that will have to wait until my jobs make it to the head of the queue on the cluster. Yes, shocking as that may seem, someone else (Brad) is using the cluster! I was getting spoiled having it all to myself. In the last 16 days since Maui has been up we've been running just under 6% efficiency. Wohoo ;). Good thing I didn't spend too much time tuning for efficiency :p.

Oh, I forgot to mention, but I've been making some changes to the simulation unrelated to the testing. Well, some of them have been related…

In the tension model utilities, you can now pick x_min and x_max when plotting energy landscapes E(x) (that was for plotting Kramers’ cusp potential). You can also pick F_max when plotting F(x).

I also ripped apart the tension-group idea and put it back together. The initial implementation was a bit embarassing. Now you can do things that tension groups are intended for, like having two seperate WLC groups (for, say, folded- and unfolded-domains).

Subversion is lots of fun, by the way ;).

I think I've spent enough time trying to find a nice analytic way to guess parameters for a Gompertz model fit to my unfolding probability densities. I now have a heuristic which seems to work :p, and I suppose I'll be satisfied with that for the time being.

On to find out about analytic solutions to Kramers' unfolding rates.

Update: I figured out how to use the NIST reference while writing my sawsim paper, listing the mean and standard deviation of the Gumbel distribution. So many names… Anyway, the pysawsim tests now use the improved guessing procedure.

The natural logarithm (log base e) used to be called the hyperbolic logarithm (see here). Other than the understandably old fasioned notation, Gompertz article is wonderfully written, so much so that I can follow all his math, even with the strange notation (although obviously I had to look hyperbolic logs up). He makes a number of brief excursions to set up the problem, including a reference to "the great age of the patriarchs of scripture". He even takes a break to clarify his exponent notation. I love this guy.

All the non-symbolic math was starting to confuse me, so I went back and Googled a bit more, turning up this paper which claims to help fit the Gompertz distribution, and even (gasp) uses the same Gompertz distribution that Gompertz does :p. It even talks about probability density functions. I dunno if I'm ready for another relationship yet though, I've been hurt so many times before ;).

This paper by Peter Pflaumer gives a bit more technical detail to the whole Gompertz/Gumbel lifespan thing. I need to remember that my model works, I just need a stable way of estimating the model parameters from which to start optimizing a fit. Pflaumer derives a formula for the mode, but it is still trancendental in the force scaling parameter.

Hmm, I should see what Garrett thinks of the economics of this distribution, since that's what it was originally developed for. He probably already knows all about it, why didn't I think to ask last weekend? Ah, because I started this on Sunday and saw him on Saturday :p.

I though this aught to do it for me, but it seems their rate has an extra -ln(P) in it. Rats.

Desperate times call for going back to Gompertz' original paper.

Aha, the probability of Bell-model unfolding under constant force-loading has a name! It is a Fisher-Tippett distribution, of which the Gumbel distribution is a particular type. However, NIST refers to it as a minimum Gumbel distribution.

Hmm, hopefully I'm not just confusing myself looking at the standardized form, let me go double check... What is a cumulative distribution function anyway? Ah, CDF(x) is just the probability that the variable will be <= x, so the probability distribution function is given by PDF(x) = -d(CDF)/dx.

Alright, looks like my distribution is a bit different than the Fisher-Tippett because I need a non-unity a factor a in PDF(x) = exp(-ax/b)*exp[-exp(x/b)] with z := exp(-x/b). Basically, I have a Fisher-Tippett distribution with a poorly scaled x, but I don't know how to rescale x until I've fit my distribution. So the search continues...

The Gompertz-Makeham Law law for exponentially increasing failure rate is what I want. But Wikipedia says this is the same as Fisher-Tippett with time inversion.

There is a nice discussion of aging in general, but not much math here.

Update: Related posts: