Node is a server-side JavaScript engine (i.e. it executes JavaScript without using a browser). This means that JavaScript developers can now develop tools in their native language, so it's not a surprise that the Bootstrap folks use Grunt for their build system. I'm new to the whole Node ecosystem, so here are my notes on how it works.

Start off by installing npm, the Node package manager. On Gentoo, that's:

# USE=npm emerge -av net-libs/nodejs

[Configure npm][npm-config] to make "global" installs in your personal space:

# npm config set prefix ~/.local/

Install the Grunt command line interface for building Bootstrap:

$ npm install -g grunt-cli

That installs the libraries under ~/.local/lib/node_modules and drops symlinks to binaries in ~/.local/bin (which is already in my PATH thanks to my dotfiles).

Clone Boostrap and install it's dependencies:

$ git clone git://github.com/twbs/bootstrap.git
$ cd bootstrap
$ npm install

This looks in the local [package.json][] to extract a list of dependencies, and installs each of them under node_modules. Node likes to isolate its packages, so every dependency for a given package is installed underneath that package. This leads to some crazy nesting:

$ find node_modules/ -name graceful-fs
node_modules/grunt/node_modules/glob/node_modules/graceful-fs
node_modules/grunt/node_modules/rimraf/node_modules/graceful-fs
node_modules/grunt-contrib-clean/node_modules/rimraf/node_modules/graceful-fs
node_modules/grunt-contrib-qunit/node_modules/grunt-lib-phantomjs/node_modules/phantomjs/node_modules/rimraf/node_modules/graceful-fs
node_modules/grunt-contrib-watch/node_modules/gaze/node_modules/globule/node_modules/glob/node_modules/graceful-fs

Sometimes the redundancy is due to different version requirements, but sometimes the redundancy is just redundant :p. Let's look with npm ls.

$ npm ls graceful-fs
bootstrap@3.0.0 /home/wking/src/bootstrap
├─┬ grunt@0.4.1
│ ├─┬ glob@3.1.21
│ │ └── graceful-fs@1.2.3
│ └─┬ rimraf@2.0.3
│   └── graceful-fs@1.1.14
├─┬ grunt-contrib-clean@0.5.0
│ └─┬ rimraf@2.2.2
│   └── graceful-fs@2.0.1
├─┬ grunt-contrib-qunit@0.2.2
│ └─┬ grunt-lib-phantomjs@0.3.1
│   └─┬ phantomjs@1.9.2-1
│     └─┬ rimraf@2.0.3
│       └── graceful-fs@1.1.14
└─┬ grunt-contrib-watch@0.5.3
  └─┬ gaze@0.4.1
    └─┬ globule@0.1.0
      └─┬ glob@3.1.21
        └── graceful-fs@1.2.3

Regardless of on-disk duplication, Node caches modules so a given module only loads once. If it really bothers you, you can avoid some duplicates by installing duplicated packages higher up in the local tree:

$ rm -rf node_modules
$ npm install graceful-fs@1.1.14
$ npm install
$ npm ls graceful-fs
bootstrap@3.0.0 /home/wking/src/bootstrap
├── graceful-fs@1.1.14  extraneous
├─┬ grunt@0.4.1
│ └─┬ glob@3.1.21
│   └── graceful-fs@1.2.3 
├─┬ grunt-contrib-clean@0.5.0
│ └─┬ rimraf@2.2.2
│   └── graceful-fs@2.0.1 
└─┬ grunt-contrib-watch@0.5.3
  └─┬ gaze@0.4.1
    └─┬ globule@0.1.0
      └─┬ glob@3.1.21
        └── graceful-fs@1.2.3 

This is probably not worth the trouble.

Now that we have Grunt and the Bootstrap dependencies, we can build the distributed libraries:

$ ~/src/node_modules/.bin/grunt dist
Running "clean:dist" (clean) task
Cleaning dist...OK

Running "recess:bootstrap" (recess) task
File "dist/css/bootstrap.css" created.

Running "recess:min" (recess) task
File "dist/css/bootstrap.min.css" created.
Original: 121876 bytes.
Minified: 99741 bytes.

Running "recess:theme" (recess) task
File "dist/css/bootstrap-theme.css" created.

Running "recess:theme_min" (recess) task
File "dist/css/bootstrap-theme.min.css" created.
Original: 18956 bytes.
Minified: 17003 bytes.

Running "copy:fonts" (copy) task
Copied 4 files

Running "concat:bootstrap" (concat) task
File "dist/js/bootstrap.js" created.

Running "uglify:bootstrap" (uglify) task
File "dist/js/bootstrap.min.js" created.
Original: 58543 bytes.
Minified: 27811 bytes.

Done, without errors.

Wohoo!

Unfortunately, like all language-specific packing systems, npm has trouble installing packages that aren't written in its native language. This means you get things like:

$ ~/src/node_modules/.bin/grunt
…
Running "jekyll:docs" (jekyll) task
`jekyll build` was initiated.

Jekyll output:
Warning: Command failed: /bin/sh: jekyll: command not found
 Use --force to continue.

Aborted due to warnings.

Once everybody wises up and starts writing packages for Gentoo Prefix, we can stop worrying about installation and get back to work developing :p.

A while back I posted about Comcast blocking outgoing traffic on port 25. We've spent some time with Verizon's DSL service, but after our recent move we're back with Comcast. Luckily, Comcast now explicitly lists the ports they block. Nothing I care about, except for port 25 (incoming and outgoing). For incoming mail, I use Dyn to forward mail to port 587. For outgoing mail, I had been using stunnel through outgoing.verizon.net for my SMTP connections. Comcast takes a similar approach forcing outgoing mail through port 465 on smtp.comcast.net.

I like Git submodules quite a bit, but they often get a bad rap. Most of the problems involve bad git hygiene (e.g. not developing in feature branches) or limitations in the current submodule implementation (e.g. it's hard to move submodules). Other problems involve not being able to fetch submodules with git:// URLs (due to restrictive firewalls).

This last case is easily solved by using relative submodule URLs in .gitmodules. I've been through the relative-vs.-absolute URL argument a few times now, so I thought I'd write up my position for future reference. I prefer the relative URL in:

[submodule "some-name"]
  path = some/path
  url = ../submod-repo.git

to the absolute URL in:

[submodule "some-name"]
  path = some/path
  url = git://example.net/submod-repo.git

Arguments in favor of relative URLs:

• Users get submodules over their preferred transport (ssh://, git://, https://, …). Whatever transport you used to clone the superproject will be recycled when you use submodule init to set submodule URLs in your .git/config.
• No need to tweak .gitmodules if you mirror (or move) your superproject Git hosting somewhere else (e.g. from example.net to elsewhere.com).
• As a special case of the mirror/move situation, there's no need to tweak .gitmodules in long-term forks. If I setup a local version of the project and host it on my local box, my lab-mates can clone my local superproject and use my local submodules without my having to alter .gitmodules. Reducing trivial differences between forks makes collaboration on substantive changes more likely.

The only argument I've heard in favor of absolute URLs is Brian Granger's GitHub workflow:

• If a user forks upstream/repo to username/repo and then clones their fork for local work, relative submodule URLs will not work until they also fork the submodules into username/.

This workflow needs absolute URLs:

But relative URLs are fine if you also fork the submodule(s):

Personally, I only create a public repository (username/repo) after cloning the central repository (upstream/repo). Several projects I contribute too (such as Git itself) prefer changes via send-email, in which case there is no need for contributors to create public repositories at all. Relative URLs are also fine here:

Once you understand the trade-offs, picking absolute/relative is just a political/engineering decision. I don't see any benefit to the absolute-URL-only repo relationship, so I favor relative URLs. The IPython folks felt that too many devs already used the absolute-URL-only relationship, and that the relative-URL benefits were not worth the cost of retraining those developers. `

Over at Software Carpentry, Greg Wilson just posted some thoughts about a hypothetical open science framework. He uses Ruby on Rails and similar web frameworks as examples where frameworks can leverage standards and conventions to take care of most of the boring boilerplate that has to happen for serving a website. Greg points out that it would be useful to have a similar open science framework that small projects could use to get off the ground and collaborate more easily.

My thesis is about developing an open source framework for single molecule force spectroscopy, so this is an avenue I'm very excited about. However, it's difficult to get this working for experimental labs with a diversity of the underlying hardware. If different labs have different hardware, it's hard to write a generic software stack that works for everybody (at least at the lower levels of the stack). Our lab does analog control and aquisition via an old National Instruments card. NI no longer sells this card, and developing Comedi drivers for new cards is too much work for many to take on pro bono. This means that new labs that want to use my software can't get started with off the shelf components; they'll need to find a second-hand card or rework the lower layers of my stack to work with a DAQ card that they can source.

I'd be happy to see an inexpensive, microprocessor-based open hardware project for synchronized, multi-channel, near-MHz analog I/O to serve as a standard interface between software and the real world, but that's not the sort of thing I can whip out over a free weekend (although I have dipped my toe in the water). I think the missing component is a client-side version of libusb, to allow folks to write the firmware for the microprocessor without dealing with the intricacies of the USB specs. It would also be nice to have a standard USB protocol for Comedi commands, so a single driver could interface with commodity DAQ hardware—much like the current situation for mice, keyboards, webcams, and other approved classes. Then the software stack could work unchanged on any hardware, once the firmware supporting the hardware had been ported to a new microprocessor. There are two existing classes (a physical interface device class and a test and measurement class), but I haven't had time to dig through those with an eye toward Comedi integration yet. So much to do, so little time…

NOAA has a Historical Map & Chart Collection with free downloads of high resolution scans of all sorts of historical maps and charts. For example, George Vancouver's 1791 “Chart Shewing part of the Coast of N.W. America”.

Lex Nederbragt posted a question about version control and provenance on the Software Carpentry discussion list. I responded with my Portage-based workflow, but C. Titus Brown pointed out a number of reasons why this approach isn't more widely used, which seem to boil down to “that sounds like more trouble than it's worth”. Because recording the state of a system is important for reproducible research, it is worth doing something to clean up the current seat-of-the-pants approach.

Figuring out what software you have intalled on your system is actually a (mostly) solved problem. There is a long history in the Linux ecosystem for package management systems that track installed packages and install new software (and any dependencies) automatically. Unfortunately, there is not a consensus package manager across distributions, with Debian-based distributions using apt, Fedora-based distributions using yum, …. If you are not the system administrator for your computer, you can either talk your sysadmin into installing the packages you need, or use one of a number of guest package managers (Gentoo Prefix, homebrew, …). The guest package managers also work if you're committed to an OS that doesn't have an existing native package manager.

Despite the existence of many high quality package managers, I know many people who continue to install significant amounts of software by hand. While this is sustainable for a handful of packages, I see no reason to struggle through manual installations (subsequent upgrades, dependencies, …) when existing tools can automate the procedure. A stopgap solution is to use language specific package managers (pip for Python, gem for Ruby, …). This works fairly well, but once you reach a certain level of complexity (e.g. integrating Fortran and C extensions with Python in SciPy), things get difficult. While language-specific packaging standards ease automation, they are not a substitute for a language-agnostic package manager.

Many distributions distribute pre-compiled, binary packages, which give fast, stable installs without the need to have a full build system on your local machine. When the package you need is in the official repository (or a third-party repository), this approach works quite well. There's no need to go through the time or effort of compiling Firefox, LaTeX, LibreOffice, or other software that I interact with as a general a user. However, my own packages (or actively developed libraries that use from my own software) are rarely available as pre-compiled binaries. If you find yourself in this situation, it is useful to use a package manager that makes it easy to write source-based packages (Gentoo's Portage, Exherbo's Paludis, Arch's packman, …).

With source-based packaging systems, packaging an existing Python package is usually a matter of listing a bit of metadata. With layman, integrating your local packages into your Portage tree is extremely simple. Does your package depend on some other package in another oddball language? Some wonky build tool? No problem! Just list the new dependency in your ebuild (it probably already exists). Source-based package managers also make it easy to stay up to date with ongoing development. Portage supports live ebuilds that build fresh checkouts from a project's version control repository (use Git!). There is no need to dig out your old installation notes or reread the projects installation instructions.

Getting back to the goals of reproducible research, I think that existing package managers are an excellent solution for tracking the software used to perform experiments or run simulations and analysis. The main stumbling block is the lack of market penetration ;). Building a lightweight package manager that can work easily at both the system-wide and per-user levels across a range of host OSes is hard work. With the current fractured packaging ecosystem, I doubt that rolling a new package manager from scratch would be an effective approach. Existing package managers have mostly satisfied their users, and the fundamental properties haven't changed much in over a decade. Writing a system appealing enough to drag these satisfied users over to your new system is probably not going to happen.

Portage (and Gentoo Prefix) get you most of the way there, with the help of well written specifications and documentation. However, compatibility and testing in the prefix configuration still need some polishing, as does robust binary packaging support. These issues are less interesting to most Portage developers, as they usually run Portage as the native package manager and avoid binary packages. If the broader scientific community is interested in sustainable software, I think effort channeled into polishing these use-cases would be time well spent.

For those less interested in adopting a full-fledged package manager, you should at least make some effort to package your software. I have used software that didn't even have a README with build instructions, but compiling it was awful. If you're publishing your software in the hopes that others will find it, use it, and cite you in their subsequent paper, it behooves you to make the installation as easy as possible. Until your community coalesces around a single package management framework, picking a standard build system (Autotools, Distutils, …) will at least make it easier for folks to install your software by hand.

Available in a git repository.
Repository: rss2email
Browsable repository: rss2email
Author: W. Trevor King

Since November 2012 I've been maintaining rss2email, a package that converts RSS or Atom feeds to email so you can follow them with your mail user agent. Rss2email was created by the late Aaron Swartz and maintained for several years by Lindsey Smith. I've added a mailing list (hosted with mlmmj) and PyPI package and made the GitHub location the homepage.

Overall, setting up the standard project infrastructure has been fun, and it's nice to see interest in the newly streamlined code picking up. The timing also works out well, since the demise of Google Reader may push some talented folks in our direction. I'm not sure how visible rss2email is, especially the fresh development locations, hence this post ;). If you know anyone who might be interested in using (or contributing to!) rss2email, please pass the word.

I've been trying to wrap my head around factor analysis as a theory for designing and understanding test and survey results. This has turned out to be another one of those fields where the going has been a bit rough. I think the key factors in making these older topics difficult are:

• “Everybody knows this, so we don't need to write up the details.”
• “Hey, I can do better than Bob if I just tweak this knob…”
• “I'll just publish this seminal paper behind a paywall…”

The resulting discussion ends up being overly complicated, and it's hard for newcomers to decide if people using similar terminology are in fact talking about the same thing.

Some of the better open sources for background has been Tucker and MacCallum's “Exploratory Factor Analysis” manuscript and Max Welling's notes. I'll use Welling's terminology for this discussion.

The basic idea of factor analsys is to model $d$ measurable attributes as generated by $k<d$ common factors and $d$ unique factors. With $n=4$ and $k=2$, you get something like:

Relationships between factors and measured attributes (adapted from Tucker and MacCallum's Figure 1.2)

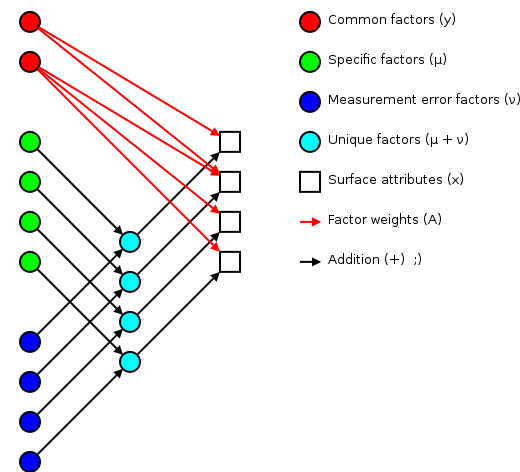Corresponding to the equation (Welling's eq. 1):

The independent random variables $y$ are distributed according to a Gaussian with zero mean and unit variance ${𝒢}_y[0,I]$ (zero mean because constant offsets are handled by $\mu$; unit variance because scaling is handled by $A$). The independent random variables $\nu$ are distributed according to ${𝒢}_{\nu }[0,\Sigma ]$, with (Welling's eq. 2):

The matrix $A$ (linking common factors with measured attributes \mathbf{\mu}$,\mathrm{we}\mathrm{can}\mathrm{calculate}\mathrm{it}\mathrm{by}\mathrm{averaging}\mathrm{out}\mathrm{the}\mathrm{random}\mathrm{noise}(\mathrm{Welling}\prime s\mathrm{eq}.6):\text{Unknown character}\mathrm{div}\mathrm{class}=\text{Unknown character}\mathrm{numberedEq}\text{Unknown character}\text{Unknown character}\text{Unknown character}\mathrm{span}\text{Unknown character}(3)\text{Unknown character}/\mathrm{span}\text{Unknown character}$$\mu =\frac{1}{N}{\sum }_{n=1}^N{x}_n$$\text{Unknown character}/\mathrm{div}\text{Unknown character}\mathrm{where}$N$\mathrm{is}\mathrm{the}\mathrm{number}\mathrm{of}\mathrm{measurements}(\mathrm{survey}\mathrm{responders})\mathrm{and}$\mathbf{x}n$\mathrm{is}\mathrm{the}\mathrm{response}\mathrm{vector}\mathrm{for}\mathrm{the}$n^\text{th}$\mathrm{responder}.\mathrm{How}\mathrm{do}\mathrm{we}\mathrm{find}$\mathbf{A}$\mathrm{and}$\mathbf{\Sigma}$?\mathrm{This}\mathrm{is}\mathrm{the}\mathrm{tricky}\mathrm{bit},\mathrm{and}\mathrm{there}\mathrm{are}a\mathrm{number}\mathrm{of}\mathrm{possible}\mathrm{approaches}.\mathrm{Welling}\mathrm{suggests}\mathrm{using}\mathrm{expectation}\mathrm{maximization}(\mathrm{EM}),\mathrm{and}\mathrm{there}\prime s\mathrm{an}\mathrm{excellent}\mathrm{example}\mathrm{of}\mathrm{the}\mathrm{procedure}\mathrm{with}a\mathrm{colorblind}\mathrm{experimenter}\mathrm{drawing}\mathrm{colored}\mathrm{balls}\mathrm{in}\mathrm{his}[\mathrm{EM}\mathrm{notes}][\mathrm{EM}](\mathrm{to}\mathrm{test}\mathrm{my}\mathrm{understanding},I\mathrm{wrote}\text{Unknown character}a\mathrm{href}=\text{Unknown character}./\mathrm{posts}/{\mathrm{Factor}}_{\mathrm{analysis}}/\mathrm{color}-\mathrm{ball}.\mathrm{py}\text{Unknown character}\text{Unknown character}\mathrm{color}-\mathrm{ball}.\mathrm{py}\text{Unknown character}/a\text{Unknown character}).\mathrm{To}\mathrm{simplify}\mathrm{calculations},\mathrm{Welling}\mathrm{defines}(\mathrm{before}\mathrm{eq}.15):\text{Unknown character}\mathrm{div}\mathrm{class}=\text{Unknown character}\mathrm{numberedEq}\text{Unknown character}\text{Unknown character}\text{Unknown character}\mathrm{span}\text{Unknown character}(4)\text{Unknown character}/\mathrm{span}\text{Unknown character}$$\begin{array}{rl}A\prime & \equiv [A,\mu ]\\ y\prime & \equiv [y^T,1{]}^T\end{array}$$\text{Unknown character}/\mathrm{div}\text{Unknown character}\mathrm{which}\mathrm{reduce}\mathrm{the}\mathrm{model}\mathrm{to}\text{Unknown character}\mathrm{div}\mathrm{class}=\text{Unknown character}\mathrm{numberedEq}\text{Unknown character}\text{Unknown character}\text{Unknown character}\mathrm{span}\text{Unknown character}(5)\text{Unknown character}/\mathrm{span}\text{Unknown character}$$x=A\prime y\prime +\nu$$\text{Unknown character}/\mathrm{div}\text{Unknown character}\mathrm{After}\mathrm{some}\mathrm{manipulation}\mathrm{Welling}\mathrm{works}\mathrm{out}\mathrm{the}\mathrm{maximizing}\mathrm{updates}(\mathrm{eq}\prime \mathrm{ns}16\mathrm{and}17):\text{Unknown character}\mathrm{div}\mathrm{class}=\text{Unknown character}\mathrm{numberedEq}\text{Unknown character}\text{Unknown character}\text{Unknown character}\mathrm{span}\text{Unknown character}(6)\text{Unknown character}/\mathrm{span}\text{Unknown character}$$\begin{array}{rl}A{\prime }^{\text{new}}& =({\sum }_{n=1}^N{x}_{n}E[y\prime \mid x_n{]}^T){({\sum }_{n=1}^N{x}_{n}E[y\prime y{\prime }^T\mid x_n])}^{-1}\\ {\Sigma }^{\text{new}}& =\frac{1}{N}{\sum }_{n=1}^N\text{diag}[x_n{x}_n^T-A{\prime }^{\text{new}}E[y\prime \mid x_n]x_n^T]\end{array}$$\text{Unknown character}/\mathrm{div}\text{Unknown character}\mathrm{The}\mathrm{expectation}\mathrm{values}\mathrm{used}\mathrm{in}\mathrm{these}\mathrm{updates}\mathrm{are}\mathrm{given}\mathrm{by}(\mathrm{Welling}\prime s\mathrm{eq}\prime \mathrm{ns}12\mathrm{and}13):\text{Unknown character}\mathrm{div}\mathrm{class}=\text{Unknown character}\mathrm{numberedEq}\text{Unknown character}\text{Unknown character}\text{Unknown character}\mathrm{span}\text{Unknown character}(7)\text{Unknown character}/\mathrm{span}\text{Unknown character}$$\begin{array}{rl}E[y\mid x_n]& =A^T(A{A}^T+\Sigma {)}^{-1}(x_n-\mu )\\ E[y{y}^T\mid x_n]& =I-A^T(A{A}^T+\Sigma {)}^{-1}A+E[y\mid x_n]E[y\mid x_n{]}^T\end{array}$$\text{Unknown character}/\mathrm{div}\text{Unknown character}\mathrm{Survey}\mathrm{analysis}===============\mathrm{Enough}\mathrm{abstraction}!\mathrm{Let}\prime s\mathrm{look}\mathrm{at}\mathrm{an}\mathrm{example}:[\mathrm{survey}\mathrm{results}][\mathrm{survey}]:\text{Unknown character}\text{Unknown character}\text{Unknown character}\mathrm{import}\mathrm{numpy}\text{Unknown character}\text{Unknown character}\text{Unknown character}\mathrm{scores}=\mathrm{numpy}.\mathrm{genfromtxt}(\prime {\mathrm{Factor}}_{\mathrm{analysis}}/\mathrm{survey}.\mathrm{data}\prime ,\mathrm{delimiter}=\prime t\prime )\text{Unknown character}\text{Unknown character}\text{Unknown character}\mathrm{scores}\mathrm{array}([[1.,3.,4.,6.,7.,2.,4.,5.],[2.,3.,4.,3.,4.,6.,7.,6.],[4.,5.,6.,7.,7.,2.,3.,4.],[3.,4.,5.,6.,7.,3.,5.,4.],[2.,5.,5.,5.,6.,2.,4.,5.],[3.,4.,6.,7.,7.,4.,3.,5.],[2.,3.,6.,4.,5.,4.,4.,4.],[1.,3.,4.,5.,6.,3.,3.,4.],[3.,3.,5.,6.,6.,4.,4.,3.],[4.,4.,5.,6.,7.,4.,3.,4.],[2.,3.,6.,7.,5.,4.,4.,4.],[2.,3.,5.,7.,6.,3.,3.,3.]])<code>\mathrm{scores}[i,j]</code>\mathrm{is}\mathrm{the}\mathrm{answer}\mathrm{the}<code>i</code>\mathrm{th}\mathrm{respondent}\mathrm{gave}\mathrm{for}\mathrm{the}<code>j</code>\mathrm{th}\mathrm{question}.\mathrm{We}\prime \mathrm{re}\mathrm{looking}\mathrm{for}\mathrm{underlying}\mathrm{factors}\mathrm{that}\mathrm{can}\mathrm{explain}\mathrm{covariance}\mathrm{between}\mathrm{the}\mathrm{different}\mathrm{questions}.\mathrm{Do}\mathrm{the}\mathrm{question}\mathrm{answers}($\mathbf{x}$)\mathrm{represent}\mathrm{some}\mathrm{underlying}\mathrm{factors}($\mathbf{y}$)?\mathrm{Let}\prime s\mathrm{start}\mathrm{off}\mathrm{by}\mathrm{calculating}$\mathbf{\mu}$:\text{Unknown character}\text{Unknown character}\text{Unknown character}\mathrm{def}{\mathrm{print}}_{\mathrm{row}}(\mathrm{row}):...\mathrm{print}(\prime \prime .\mathrm{join}(\prime :0.2f\prime .\mathrm{format}(x)\mathrm{for}x\mathrm{in}\mathrm{row}))\text{Unknown character}\text{Unknown character}\text{Unknown character}\mathrm{mu}=\mathrm{scores}.\mathrm{mean}(\mathrm{axis}=0)\text{Unknown character}\text{Unknown character}\text{Unknown character}{\mathrm{print}}_{\mathrm{row}}(\mathrm{mu})2.423.585.085.756.083.423.924.25\mathrm{Next}\mathrm{we}\mathrm{need}\mathrm{priors}\mathrm{for}$\mathbf{A}$\mathrm{and}$\mathbf{\Sigma}$.\text{Unknown character}\mathrm{span}\mathrm{class}=\text{Unknown character}\mathrm{createlink}\text{Unknown character}\text{Unknown character}\mathrm{MDP}\text{Unknown character}/\mathrm{span}\text{Unknown character}\mathrm{has}\mathrm{an}\mathrm{implementation}\mathrm{for}\text{Unknown character}a\mathrm{href}=\text{Unknown character}./\mathrm{posts}/\mathrm{Python}/\text{Unknown character}\text{Unknown character}\mathrm{Python}\text{Unknown character}/a\text{Unknown character},\mathrm{and}\mathrm{their}[\mathrm{FANode}][]\mathrm{uses}a\mathrm{Gaussian}\mathrm{random}\mathrm{matrix}\mathrm{for}$\mathbf{A}$\mathrm{and}\mathrm{the}\mathrm{diagonal}\mathrm{of}\mathrm{the}\mathrm{score}\mathrm{covariance}\mathrm{for}$\mathbf{\Sigma}$.\mathrm{They}\mathrm{also}\mathrm{use}\mathrm{the}\mathrm{score}\mathrm{covariance}\mathrm{to}\mathrm{avoid}\mathrm{repeated}\mathrm{summations}\mathrm{over}$n$.\text{Unknown character}\text{Unknown character}\text{Unknown character}\mathrm{import}\mathrm{mdp}\text{Unknown character}\text{Unknown character}\text{Unknown character}\mathrm{def}{\mathrm{print}}_{\mathrm{matrix}}(\mathrm{matrix}):...\mathrm{for}\mathrm{row}\mathrm{in}\mathrm{matrix}:...{\mathrm{print}}_{\mathrm{row}}(\mathrm{row})\text{Unknown character}\text{Unknown character}\text{Unknown character}\mathrm{fa}=\mathrm{mdp}.\mathrm{nodes}.\mathrm{FANode}({\mathrm{output}}_{\dim }=3)\text{Unknown character}\text{Unknown character}\text{Unknown character}\mathrm{numpy}.\mathrm{random}.\mathrm{seed}(1)\#\mathrm{for}\mathrm{consistend}\mathrm{doctest}\mathrm{results}\text{Unknown character}\text{Unknown character}\text{Unknown character}{\mathrm{responder}}_{\mathrm{scores}}=\mathrm{fa}(\mathrm{scores})\#\mathrm{common}\mathrm{factors}\mathrm{for}\mathrm{each}\mathrm{responder}\text{Unknown character}\text{Unknown character}\text{Unknown character}{\mathrm{print}}_{\mathrm{matrix}}({\mathrm{responder}}_{\mathrm{scores}})-1.92-0.450.000.671.971.960.700.03-2.000.290.03-0.60-1.021.79-1.430.820.27-0.23-0.07-0.080.82-1.38-0.270.480.79-1.170.501.59-0.30-0.410.01-0.480.73-0.46-1.340.18\text{Unknown character}\text{Unknown character}\text{Unknown character}{\mathrm{print}}_{\mathrm{row}}(\mathrm{fa}.\mathrm{mu}.\mathrm{flat})2.423.585.085.756.083.423.924.25\text{Unknown character}\text{Unknown character}\text{Unknown character}\mathrm{fa}.\mathrm{mu}.\mathrm{flat}==\mathrm{mu}\#\mathrm{MDP}\mathrm{agrees}\mathrm{with}\mathrm{our}\mathrm{earlier}\mathrm{calculation}\mathrm{array}([\mathrm{True},\mathrm{True},\mathrm{True},\mathrm{True},\mathrm{True},\mathrm{True},\mathrm{True},\mathrm{True}],\mathrm{dtype}=\mathrm{bool})\text{Unknown character}\text{Unknown character}\text{Unknown character}{\mathrm{print}}_{\mathrm{matrix}}(\mathrm{fa}.A)\#\mathrm{factor}\mathrm{weights}\mathrm{for}\mathrm{each}\mathrm{question}0.80-0.06-0.450.170.30-0.650.34-0.13-0.250.13-0.73-0.640.02-0.32-0.700.610.230.860.080.630.59-0.090.670.13\text{Unknown character}\text{Unknown character}\text{Unknown character}{\mathrm{print}}_{\mathrm{row}}(\mathrm{fa}.\mathrm{sigma})\#\mathrm{unique}\mathrm{noise}\mathrm{for}\mathrm{each}\mathrm{question}0.040.020.380.550.300.050.480.21\mathrm{Because}\mathrm{the}\mathrm{covariance}\mathrm{is}\mathrm{unaffected}\mathrm{by}\mathrm{the}\mathrm{rotation}$\mathbf{A}\rightarrow\mathbf{A}\mathbf{R}$,\mathrm{the}\mathrm{estimated}\mathrm{weights}$\mathbf{A}$\mathrm{and}\mathrm{responder}\mathrm{scores}$\mathbf{y}$\mathrm{can}\mathrm{be}\mathrm{quite}\mathrm{sensitive}\mathrm{to}\mathrm{the}\mathrm{seed}\mathrm{priors}.\mathrm{The}\mathrm{width}$\mathbf{\Sigma}$\mathrm{of}\mathrm{the}\mathrm{unique}\mathrm{noise}$\mathbf{\nu}$\mathrm{is}\mathrm{more}\mathrm{robust},\mathrm{because}$\mathbf{\Sigma}$\mathrm{is}\mathrm{unaffected}\mathrm{by}\mathrm{rotations}\mathrm{on}$\mathbf{A}$.\mathrm{Related}\mathrm{tidbits}===============\mathrm{Communality}-----------\mathrm{The}[\mathrm{communality}][]$hi^2$\mathrm{of}\mathrm{the}$i^\text{th}$\mathrm{measured}\mathrm{attribute}$x_i$\mathrm{is}\mathrm{the}\mathrm{fraction}\mathrm{of}\mathrm{variance}\mathrm{in}\mathrm{the}\mathrm{measured}\mathrm{attribute}\mathrm{which}\mathrm{is}\mathrm{explained}\mathrm{by}\mathrm{the}\mathrm{set}\mathrm{of}\mathrm{common}\mathrm{factors}.\mathrm{Because}\mathrm{the}\mathrm{common}\mathrm{factors}$\mathbf{y}$\mathrm{have}\mathrm{unit}\mathrm{variance},\mathrm{the}\mathrm{communality}\mathrm{is}\mathrm{given}\mathrm{by}:\text{Unknown character}\mathrm{div}\mathrm{class}=\text{Unknown character}\mathrm{numberedEq}\text{Unknown character}\text{Unknown character}\text{Unknown character}\mathrm{span}\text{Unknown character}(8)\text{Unknown character}/\mathrm{span}\text{Unknown character}$$h_i=\frac{{\sum }_{j=1}^k{A}_{\mathrm{ij}}^2}{{\sum }_{j=1}^k{A}_{\mathrm{ij}}^2+{\sigma }_1^2}$\mathbf{A}$\mathrm{and}\Sigma$ and the variations contained in the measured scores (why?):

>>> print_row(factor_variance + fa.sigma)
 0.89   0.56   0.57   1.51   0.89   1.21   1.23   0.69
>>> print_row(scores.var(axis=0, ddof=1))  # total variance for each question
 0.99   0.63   0.63   1.66   0.99   1.36   1.36   0.75

The proportion of total variation explained by the common factors is given by:

Varimax rotation

As mentioned earlier, factor analysis generated loadings $A$ that are unique up to an arbitrary rotation $R$ (as you'd expect for a $k$-dimensional Gaussian ball of factors $y$). A number of of schemes have been proposed to simplify the initial loadings by rotating $A$ to reduce off-diagonal terms. One of the more popular approaches is Henry Kaiser's varimax rotation (unfortunately, I don't have access to either his thesis or the subsequent paper). I did find (via Wikipedia) Trevor Park's notes which have been very useful.

The idea is to iterate rotations to maximize the raw varimax criterion (Park's eq. 1):

Rather than computing a $k$-dimensional rotation in one sweep, we'll iterate through 2-dimensional rotations (on successive column pairs) until convergence. For a particular column pair $(p,q)$, the rotation matrix $R^{*}$ is the usual rotation matrix:

where the optimum rotation angle ${\varphi }^{*}$ is (Park's eq. 3):

where $i\equiv \sqrt{-1}$.

Nomenclature

$A_{\mathrm{ij}}$

The element from the $i^{\text{th}}$ row and $j^{\text{th}}$ column of a matrix $A$. For example here is a 2-by-3 matrix terms of components:

(13)$$A=\left(\begin{array}{ccc}{A}_{11}& A_{12}& A_{13}\\ A_{21}& A_{22}& A_{23}\end{array}\right)$$

$A^T$

The transpose of a matrix (or vector) $A$. $A_{\mathrm{ij}}^T=A_{\mathrm{ji}}$

$A^{-1}$

The inverse of a matrix $A$. $A^{-1}\dot{A}=1$

$\text{diag}[A]$

A matrix containing only the diagonal elements of $A$, with the off-diagonal values set to zero.

$E[f(x)]$

Expectation value for a function $f$ of a random variable $x$. If the probability density of $x$ is $p(x)$, then $E[f(x)]=\int dxp(x)f(x)$. For example, $E[p(x)]=1$.

$\mu$

The mean of a random variable $x$ is given by $\mu =E[x]$.

$\Sigma$

The covariance of a random variable $x$ is given by $\Sigma =E[(x-\mu )(x-\mu {)}^T]$. In the factor analysis model discussed above, $\Sigma$ is restricted to a diagonal matrix.

${𝒢}_x[\mu ,\Sigma ]$

A Gaussian probability density for the random variables $x$ with a mean $\mu$ and a covariance $\Sigma$.

(14)$${𝒢}_x[\mu ,\Sigma ]=\frac{1}{(2\pi {)}^{\frac{D}{2}}\sqrt{\det [\Sigma ]}}{e}^{-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )}$$

$p(y\mid x)$

Probability of $y$ occurring given that $x$ occured. This is commonly used in Bayesian statistics.

$p(x,y)$

Probability of $y$ and $x$ occuring simultaneously (the joint density). $p(x,y)=p(x\mid y)p(y)$

$\angle (z)$

The angle of $z$ in the complex plane. $\angle ({\mathrm{re}}^{i\theta })=\theta$.

Note: if you have trouble viewing some of the more obscure Unicode used in this post, you might want to install the STIX fonts.

Available in a git repository.
Repository: catalyst-swc
Browsable repository: catalyst-swc
Author: W. Trevor King

Catalyst is a release-building tool for Gentoo. If you use Gentoo and want to roll your own live CD or bootable USB drive, this is the way to go. As I've been wrapping my head around catalyst, I've been pushing my notes upstream. This post builds on those notes to discuss the construction of a bootable ISO for Software Carpentry boot camps.

Getting a patched up catalyst

Catalyst has been around for a while, but the user base has been fairly small. If you try to do something that Gentoo's Release Engineering team doesn't do on a regular basis, built in catalyst support can be spotty. There's been a fair amount of patch submissions an gentoo-catalyst@ recently, but patch acceptance can be slow. For the SWC ISO, I applied versions of the following patches (or patch series) to 37540ff:

• chmod +x all sh scripts so they can run from the git checkout
• livecdfs-update.sh: Set XSESSION in /etc/env.d/90xsession
• Fix livecdfs-update.sh startx handling

Configuring catalyst

The easiest way to run catalyst from a Git checkout is to setup a local config file. I didn't have enough hard drive space on my local system (~16 GB) for this build, so I set things up in a temporary directory on an external hard drive:

$ cat catalyst.conf | grep -v '^#\|^$'
digests="md5 sha1 sha512 whirlpool"
contents="auto"
distdir="/usr/portage/distfiles"
envscript="/etc/catalyst/catalystrc"
hash_function="crc32"
options="autoresume kerncache pkgcache seedcache snapcache"
portdir="/usr/portage"
sharedir="/home/wking/src/catalyst"
snapshot_cache="/mnt/d/tmp/catalyst/snapshot_cache"
storedir="/mnt/d/tmp/catalyst"

I used the default values for everything except sharedir, snapshot_cache, and storedir. Then I cloned the catalyst-swc repository into /mnt/d/tmp/catalyst.

Portage snapshot and a seed stage

Take a snapshot of the current Portage tree:

# catalyst -c catalyst.conf --snapshot 20130208

Download a seed stage3 from a Gentoo mirror:

# wget -O /mnt/d/tmp/catalyst/builds/default/stage3-i686-20121213.tar.bz2 \
>   http://distfiles.gentoo.org/releases/x86/current-stage3/stage3-i686-20121213.tar.bz2

Building the live CD

# catalyst -c catalyst.conf -f /mnt/d/tmp/catalyst/spec/default-stage1-i686-2013.1.spec
# catalyst -c catalyst.conf -f /mnt/d/tmp/catalyst/spec/default-stage2-i686-2013.1.spec
# catalyst -c catalyst.conf -f /mnt/d/tmp/catalyst/spec/default-stage3-i686-2013.1.spec
# catalyst -c catalyst.conf -f /mnt/d/tmp/catalyst/spec/default-livecd-stage1-i686-2013.1.spec
# catalyst -c catalyst.conf -f /mnt/d/tmp/catalyst/spec/default-livecd-stage2-i686-2013.1.spec

isohybrid

To make the ISO bootable from a USB drive, I used isohybrid:

# cp swc-x86.iso swc-x86-isohybrid.iso
# isohybrid iso-x86-isohybrid.iso

You can install the resulting ISO on a USB drive with:

# dd if=iso-x86-isohybrid.iso of=/dev/sdX

replacing replacing X with the appropriate drive letter for your USB drive.

With versions of catalyst after d1c2ba9, the isohybrid call is built into catalysts ISO construction.

SymPy is a Python library for symbolic mathematics. To give you a feel for how it works, lets extrapolate the extremum location for $f(x)$ given a quadratic model:

and three known values:

Rephrase as a matrix equation:

So the solutions for $A$, $B$, and $C$ are:

Now that we've found the model parameters, we need to find the $x$ coordinate of the extremum.

which is zero when

Here's the solution in SymPy:

>>> from sympy import Symbol, Matrix, factor, expand, pprint, preview
>>> a = Symbol('a')
>>> b = Symbol('b')
>>> c = Symbol('c')
>>> fa = Symbol('fa')
>>> fb = Symbol('fb')
>>> fc = Symbol('fc')
>>> M = Matrix([[a**2, a, 1], [b**2, b, 1], [c**2, c, 1]])
>>> F = Matrix([[fa],[fb],[fc]])
>>> ABC = M.inv() * F
>>> A = ABC[0,0]
>>> B = ABC[1,0]
>>> x = -B/(2*A)
>>> x = factor(expand(x))
>>> pprint(x)
 2       2       2       2       2       2   
a *fb - a *fc - b *fa + b *fc + c *fa - c *fb
---------------------------------------------
 2*(a*fb - a*fc - b*fa + b*fc + c*fa - c*fb) 
>>> preview(x, viewer='pqiv')

Where pqiv is the executable for pqiv, my preferred image viewer. With a bit of additional factoring, that is: