My wife was recently reviewing some pulse oxymeter notes while working a round of anesthesia. It took us a while to trace the logic through all the symbol changes and notation shifts, and my wife's math-discomfort and my bio-discomfort made us more cautious than it turns out we needed to be. There are a number of nice review articles out there that I turned up while looking for explicit derivations, but by the time I'd found them, my working notes had gotten fairly well polished themselves. So here's my contribution to the pulse-ox noise ;). Highlights include:

• Short and sweet (with pictures)
• Symbols table
• Baby steps during math manipulation

Oxygen content

The circulatory system distributes oxygen (O₂) throughout the body. The amount of O₂ at any given point is measured by the O₂ content ([O₂]), usually given in $\frac{\text{mL O₂ at BTP}}{\text{dL blood}}$ (BTP is my acronym for body temperature and pressure). Most transported O₂ is bound to hemoglobin (Hb), but there is also free O₂ disolved directly in the plasma and cytoplasm of suspended cells.

where ${\text{S}}_{\text{O₂}}$ is the Hb's O₂ saturation and ${\text{P}}_{\text{O₂}}$ is the O₂ partial pressure. Don't worry about the coefficients $a$ and $b$ yet, we'll get back to them in a second.

The amound of dissolved O₂ is given by its partial pressure (${\text{P}}_{\text{O₂}}$). Partial pressures are generally given in mm of mercury (Hg) at standard temperature and pressure (STP). Because the partial pressure changes as blood flows through the body, an additional specifier $i$ may be added ($\text{P}{i}_{\text{O₂}}$) to clarify the measurement location.

O₂ is carried in the blood primarily through binding to hemoglobin monomers (Hb), with each monomer potentially binding a single O₂. Oxygen saturation (${\text{S}}_{\text{O₂}}$) is the fraction of hemoglobin monomers (Hb) that have bound an oxygen molecule (O₂).

The ratio of concentrations, ${\text{S}}_{\text{O₂}}$, is unitless. It is often expressed as a percentage. [Hb] is often given in g/dL. As with partial pressures, an additional specifier $i$ may be added ($\text{S}{i}_{\text{O₂}}$) to clarify the measurement location (${\text{Sa}}_{\text{O₂}}$, ${\text{Sp}}_{\text{O₂}}$, …).

Now we can take a second look at our O₂ content formula. The coefficient $a$ must convert g/dL to $\frac{\text{mL O₂ at BTP}}{\text{dL blood}}$. Using the molecular weight of Hb and the volume of a mole of gas at STP:

where $\chi$ is a pure number (we're just working out the unit conversion here, not converting a particular Hg concentration). Therefore, $a=1.32\frac{\text{mL O₂ at BTP}}{\text{g Hb}}$. The powers that be seem to have used a slightly different density, since the more commonly used value is 5% higher at $1.39$. Possibly someone actually measured the density of O₂ at BTP, because BTP is not STP, and O₂ is not an ideal gas.

The coefficient $b$ must convert mm Hg at STP to $\frac{\text{mL O₂ at BTP}}{\text{dL blood}}$. Empirical experiments (?) give a value of $b=0.003\frac{\text{mL O₂ at BTP}}{\text{dL blood ⋅ mm Hg at STP}}$. Now we can write out the familiar form

Reasonable levels are

Because the dissolved O₂ has such a tiny contribution (1.5% of the total in my example), it is often measured at STP rather than BTP. Sometimes it is dropped from the calculation entirely. We focus on the more imporant $\text{[Hb]}{\text{S}}_{\text{O₂}}$ in the next section.

Oxygen saturation

The preceding discussion used $\text{[Hb]}{\text{S}}_{\text{O₂}}$ to represent the concentration of HbO₂ complexes. This was useful while we were getting our bearings, but now we will replace that term with a more detailed model. Let us sort the Hb monomers into species:

• Hb: all hemoglobin monomers
• HbO₂: monomers complexed with O₂
• HHb: reduced Hb (not complexed with O₂)
• dysHb: dys-hemoglobin (cannot complex with O₂)
• MHb: methemoglobin
• HbCO: carboxyhemoglobin

These species are related as follows

Because modern two-color pulse-oximeters don't measure ${\text{S}}_{\text{O₂}}$ exactly, the related quantity that they do measure has been given a name of its own: the functional saturation (${\text{Sf}}_{\text{O₂}}$).

Rephrasing our earlier saturation, we see

To avoid confusion with ${\text{Sf}}_{\text{O₂}}$, our original ${\text{S}}_{\text{O₂}}$ is sometimes referred to as the fractional saturation.

The Beer-Labmert law

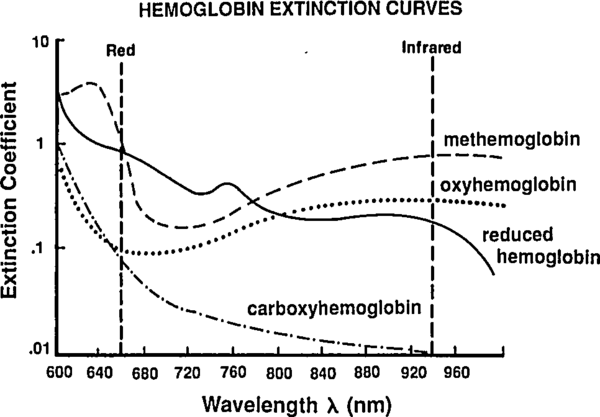
So far we've been labeling and defining attributes of the blood. The point of this excercise is to understand how a pulse oximeter measures them. People have known for a while that different hemoglobin complexes (HbO₂, HHb, MHb, HbCO, …) have differnt absorbtion spectra, and they have been using this difference since the 1930's to make pulse-oximeters based on two-color transmittance measurements (see Tremper 1989).

Absorbance spectra for assorted hemoglobin species (Tremper 1989)

By passing different wavelengths of light through perfused tissue, we can measure the relative quantities of the different Hb species. The basis for this analysis comes from the Beer-Lambert law.

where $I_0$ is the incident intensity (entering the tissue), $I$ is the tranmitted intensity (leaving the tissue), $c$ is the tissue density (concentration), $ϵ$ is the extinction coefficient (molar absorbtivity), and $L$ is the tissue thickness. Rephrasing the math as English, this means that the intensity drops off exponentially as you pass through the tissue, and more tissue (higher $c$ or $L$) or more opaque tissue (higher $ϵ$) mean you'll get less light out the far side. This is a very simple law, and the price of the simplicity is that it brushes all sorts of things under the rug. Still, it will help give us a basic idea of what is going on in a pulse-oximeter.

Rather than treat the the tissue as a single substance, lets use the Beer-Labmert law on a mixture of substances with concentrations $c_1$, $c_2$, … and extinction coefficients ${ϵ}_1$, ${ϵ}_2$, ….

We also notice that the intensities and extinction coefficients may all depend on the wavelength of light $\lambda$, so we should really write

Once isolated, a simple spectroscopy experiment can measure the extinction coefficient ${ϵ}_{i\lambda }$ of a given species across a range of $\lambda$, and this has been done for all of our common Hb flavors. We need to play with the last equation to find a way to extract the unknown concentrations, which we can then use to calculate the ${\text{Sf}}_{\text{O₂}}$ and ${\text{S}}_{\text{O₂}}$ which we can use in turn to calculate $\text{[O₂]}$.

Note that by increasing the number of LEDs (adding new $\lambda$) we increase the number of constraints on the unknown $c_i$. A traditional pulse-oximeter uses two LEDs, at 660 nm and 940 nm, to measure ${\text{Sf}}_{\text{O₂}}$ (related to [HbO₂] and [HHb]). More recent designs called pulse CO-oximeters use more wavelengths to allow measurement of quanties related to additional species (approaching the end goal of measuring ${\text{S}}_{\text{O₂}}$).

Let us deal with the fact that there is a lot of stuff absorbing light that is not arterial blood (e.g. venous blood, other tissue, bone, etc). The good thing about this stuff is that it's just sitting there or moving through in a smooth fasion. Arterial blood is the only thing that's pulsing. Here's another figure from Tremper:

AC and DC transmission components (Tremper)

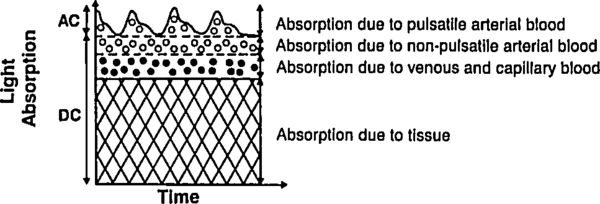During a pulse, the pressure in the finger increases and non-arterial tissue is compressed, changing $L$ and $c_i$ from their trough values to peak values $L\prime$ and $c_i\prime$. Since the finger is big, the fractional change in width $\mathrm{d}L/L=(L\prime -L)/L$ is very small. Assuming the change in concentration is even smaller (since most liquids are fairly incompressible), we have

where $X=c_1{ϵ}_{1\lambda }+c_2{ϵ}_{2labmda}+\dots$ is just a placeholder to reduce clutter. $\mathrm{d}{I}_{\lambda }$ is the AC amplitude (height of wiggle top of the detected light intensity due to pulsatile arterial blood), while $I_{\lambda }$ is the DC ampltude (height of the static base of the detected light intensity due to everything else). This is actually a fairly sneaky step, because if we can also use it to drop the DC compents. Because we've assumed fixed concentrations (incompressible fluids), and there is no more DC material coming in during a pulse (by definition), the effective $L$ for the DC components does not change. Separating the DC and AC components and running through the derivative again, we have

where $Y=e^{-(c_{\text{DC}1}{ϵ}_{\text{DC}1\lambda }+c_{\text{DC}2}{ϵ}_{\text{DC}2\lambda }+\dots )L_{\text{DC}}}$ and $Z=c_{\text{AC}1}{ϵ}_{\text{AC}1\lambda }+c_{\text{AC}2}{ϵ}_{\text{AC}2\lambda }+\dots )$ are just placeholders to reduce clutter. Note that the last equation looks just like the previous one with the translation $X\to Z$. This means that if we stick to using the AC-DC intensity ratio ($\frac{\mathrm{d}Il}{Il}$) we can forget about the DC contribution completely.

If the changing-$L$-but-static-$L_{\text{DC}}$ thing bothers you, you can imagine insteadthat $L_{\text{DC}}$ grows with $L$, but $c_{\text{DC}i}$ shrinks proportially (to conserve mass). With this proportionate stretching, there is still no change in absorbtion for that component so $\frac{\mathrm{d}}{\mathrm{d}L}\exp (-c_{\text{DC}i}{ϵ}_{\text{DC}i\lambda }L)=0$ and we can still pull the DC terms out of the integral as we just did.

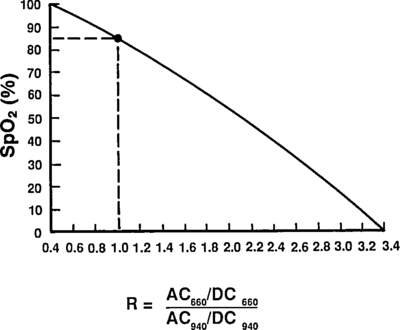
Taking a ratio of these amplitudes at two different wavelengths, we get optical density ratio (R)

because $\mathrm{d}L$ (the amount of finger expansion during a pulse) obviously doesn't depend on the color light you are using. Plugging back in for $Z$,

Assuming, for now, that there are only two species of Hb—HbO₂ and HHb—we can solve for $c_{\text{AC}1}/c_{\text{AC}2}$.

So now we know [HbO₂]/[HHb] in terms of the measured quantity $R$ and the empirical values $ϵ$.

Plugging in to our equation for ${\text{Sf}}_{\text{O₂}}$ to find the functional saturation:

As a check, we can rephrase this as

which matches Mendelson 1989, Eq. 8 with the translations:

• ${\text{Sf}}_{\text{O₂}}\to \mathrm{Sp}\text{O₂}$,
• $R\to R/\mathrm{IR}$,
• ${ϵ}_{\text{AC}\mathrm{2,660}}\to {ϵ}_R(\text{Hb})$,
• ${ϵ}_{\text{AC}\mathrm{2,940}}\to {ϵ}_{\mathrm{IR}}(\text{Hb})$,
• ${ϵ}_{\text{AC}\mathrm{1,660}}\to {ϵ}_R(\text{HbO₂})$, and
• ${ϵ}_{\text{AC}\mathrm{1,940}}\to {ϵ}_{\mathrm{IR}}(\text{HbO₂})$.

And that is the first-order explaination of how a pulse-oximeter measures the functional saturation!

Reading extinction coefficients off the absorbtion figure, I get

which are comfortingly close to those given by Mendelson in Table 1. The corresponding ${\text{Sf}}_{\text{O₂}}(R)$ plot (from Tremper) is:

Experimental SpO₂ vs. R (Tremper)

Theoretical SfO₂ vs. R.

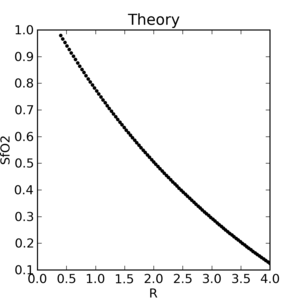The theoretical plot was calculated using SfO2vR-theory.py and our ${\text{Sf}}_{\text{O₂}}$ equation. This is why it’s a good idea to use an empirical calibration curve! The concave theoretical curve is supported by Mendelson's figure 4.

Nomenclature

O₂

Molecular oxygen

[$x$]

Concentration of $x$ in the blood

BTP

Body temperature and pressure

STP

Standard temperature and pressure

${\text{P}}_{\text{O₂}}$

O₂ partial pressure

$\text{P}{i}_{\text{O₂}}$

O₂ partial pressure at location $i$

${\text{S}}_{\text{O₂}}$

Fractional O₂ saturation

$\text{S}{i}_{\text{O₂}}$

O₂ fractional saturation at location $i$

${\text{Sf}}_{\text{O₂}}$

Functional O₂ saturation

Hg

Mercury

Hb

Hemoglobin monomer

HbO₂

Hemoglobin monomers complexed with O₂

HHb

Reduced hemoglobin (not complexed with O₂)

dysHb

Dys-hemoglobin (cannot complex with O₂)

MHb

Methemoglobin

HbCO

Carboxyhemoglobin

$I_{0\lambda }$

Intensity of incident light at wavelength $\lambda$

$I_{\lambda }$

Intensity of transmitted light at wavelength $\lambda$

$c_i$

Concentration of light-absorbing species $i$

$c_{\text{DC}i}$

Concentration of the $i$th DC species at wavelength $\lambda$

$c_{\text{AC}i}$

Concentration of the $i$th AC species at wavelength $\lambda$

${ϵ}_{i\lambda }$

Extinction coefficient of species $i$ at wavelength $\lambda$

${ϵ}_{\text{DC}i\lambda }$

Extinction coefficient of the $i$th DC species wavelength $\lambda$

${ϵ}_{\text{DC}i\lambda }$

Extinction coefficient of the $i$th DC species wavelength $\lambda$

$L$

Length of tissue through which light must pass

$L_{\text{DC}}$

Diastolic finger width

$R$

Optical density ratio

LED

Light emitting diode