Velocity clamp force spectroscopy pulls are often fit to polymer models such as the worm-like chain (WLC). However, Puchner et al. had the bright idea that, rather than fitting each loading region with a polymer model, it is easier to calculate the change in contour length by converting the abscissa to contour-length space. While the WLC is commonly used, Puchner gets better fits using the freely rotating chain (FRC) model.

Computing force-extension curves for either the WLC or FJC is complicated, and it is common to use interpolation formulas to estimate the curves. For the WLC, we use Bustamante's formula:

For the FRC, Puchner uses Livadaru's equation 46.

Unfortunately, there are two typos in Livadaru's equation 46. It should read (confirmed by private communication with Roland Netz).

Regardless of the form of Livadaru's equation 46, the suggested FRC interpolation formula is Livadaru's equation 49, which has continuous cross-overs between the various regimes and adds the possibility of elastic backbone extension.

where $l=b\frac{\cos (\gamma /2)}{\mid \ln (\cos \gamma )\mid }$ (Livadaru's equation 22) is the effective persistence length, $\beta$ determines the crossover sharpness, $\tilde{\gamma }$ is the backbone stretching modulus, and $F_{\text{WLC}}^{-1}[x]$ is related to the inverse of Bustamante's interpolation formula,

By matching their interpolation formula with simlated FRCs, Livadaru suggests using $\beta =2$, $\tilde{\gamma }=\mathrm{\infty }$, and $c=2$. In his paper, Puchner suggests using $b=0.4$ nm and $\gamma ={22}^{\circ }$. However, when I contacted him and pointed out the typos in Livadaru's equation 46, he reran his analysis and got similar results using the corrected formula with $b=0.11$ nm and $\gamma ={41}^{\circ }$. This makes more sense because it gives a WLC persistence length similar to the one he used when fitting the WLC model:

(vs. his WLC persistence length of $p=0.4$ nm).

In any event, the two models (WLC and FRC) give similar results for low to moderate forces, with the differences kicking in as $\mathrm{fb}/k_{B}T$ moves above $l/b$. For Puchner's revised numbers, this corresponds to

assuming a temperature in the range of 300 K.

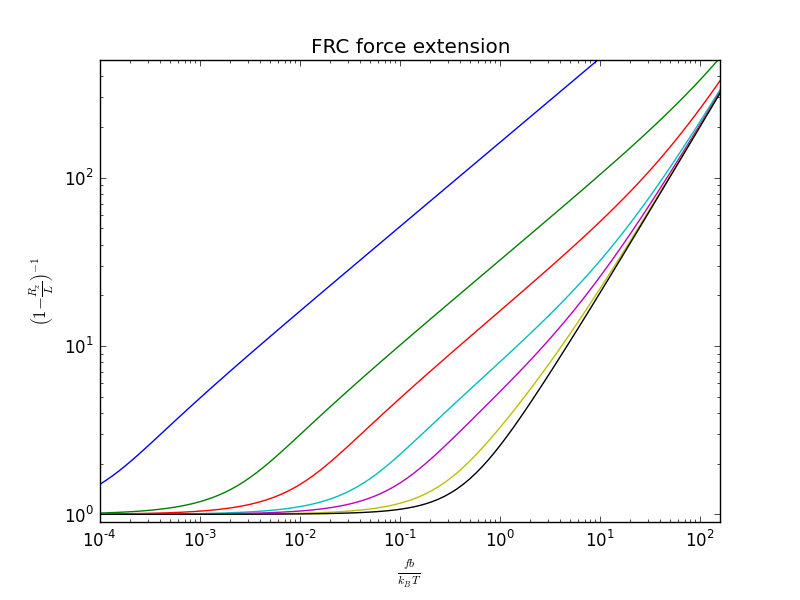
I've written an inverse_frc implementation in crunch.py for comparing velocity clamp experiments. I test the implementation with frc.py by regenerating Livadaru et al.'s figure 14.