YACC precedence and shift/reduce errors
While I was working on a BibTeX parser, I ran into some trouble with
shift/reduce errors in yacc. The problem essentially boiled down
to: How do you define implicit multiplication in yacc?
Keep reading for my intro to yacc, or, if you just want the simple
solution, skip to the end.
Related work
After much googling about, I would like to recommend the following sources:
- David Beazley's PLY documentation which has an good introduction to shift/reduce errors with a nice walkthrough shift/reduce example;
- Stephen Johnson's yacc introduction (see Section 4: How the Parser Works), which helped me understand the state-stack concept which hadn't sunk in until then;
- Leon Kaplan's yaccviso documenation, which reminded me that
visualizations are good, and inspired my resurrection of the
yacc2dottool in Python; and - Xavier Leroy et al.'s ocamlyacc documentation, where rule-vs-operator precedence finally clicked.
For further details and entertaining browsing, you can take a slow meander through the Bison manual.
Tools
The following graphics were generated from the y.output files output
by yacc using yacc2dot.py script and Graphviz dot.
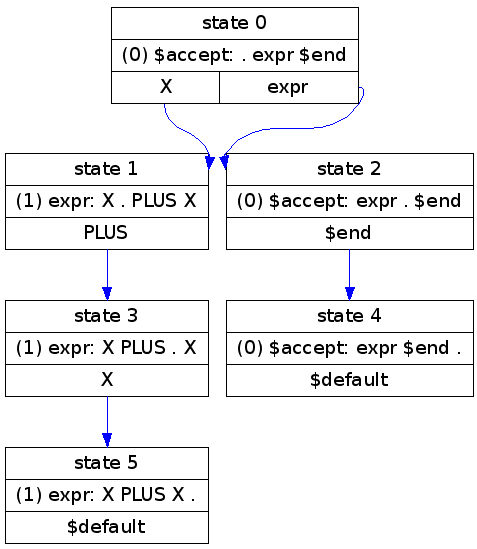
Example 1: Single, explicit addition
As a brief introduction to how parsers work, consider the really simple grammar
which generates the following yacc output and dot image:
Parsing input like X PLUS X would look like
| Step | State stack | Symbol stack | Symbol queue | Action |
|---|---|---|---|---|
| 0 | 0 | $accept | X PLUS X $end | Shift X |
| 1 | 01 | $accept X | PLUS X $end | Shift PLUS |
| 2 | 013 | $accept X PLUS | X $end | Shift X |
| 3 | 0135 | $accept X PLUS X | $end | Reduce using rule 1, pop back to state 0, and goto state 2 |
| 4 | 02 | $accept expr | $end | Shift $end |
| 5 | 024 | $accept expr $end | Accept using rule 0 |
The key step here is 3-to-4. We reduce using Rule 1
(1) expr: X PLUS X
Since there are three symbols on the rule's right hand side, we pop three symbols from the stack. The symbols we pop match the right hand side, which is why we can apply the rule. We also pop three states (1, 3, and 5), which returns us to state 0. We look up state 0's action for rules reducing to expr, and see that we're supposed to go to state 2, so we do. Whew!
It's a lot of words, and not very intuitive for me the first time around, but the underlying idea is pretty simple.
The tokens $accept and $end are inserted by the parser so it knows
if the symbols left after parsing are acceptable or not.
The input token string X PLUS X is the only valid token string for
this grammar. For extra credit, you can figure out where other input
strings go wrong. For example, consider X and X PLUS X PLUS X.
More examples
In my gradual work up to implicit multiplication, I went through the following progressively more complicated examples.
| grammar | yacc output | yacc2dot output | notes |
|---|---|---|---|
| pr.y | pr.output | pr.png | Recursive addition (allow X PLUS X PLUS X PLUS ...). Already a shift/reduce error! |
| pr prec.y | pr prec.output | pr prec.png | Add precedence (PLUS > X) to solve in favor of reduction. |
| pt.y | pt.output | pt.png | Explicit addition and multiplication with precedence. |
| t implicit.y | t implicit.output | t implicit.png | Implicit multiplication. Shift/reduce error, but no operator handle for assigning higher precedence to reduction... |
Implicit multiplication
The lack of an operator handle to assign precedence to an operator-less rule had me stumped for a few days, until I found the OCaml site with a nice, explicit listing of the shift/reduce decision process.
The shift/reduce decision is not a problem of which operator has a higher precedence, but about whether a given token has a higher precedence than a given rule. All we have to do is assign precedence to both the tokens and the rules.
which generates the following yacc output and dot image: